Skip to content

Preview Animation

👋 Welcome to Text Recovery Project

A Python library for distributed LLM training over the Internet to solve the Running Key Cipher, a well-known Cryptography problem

Nowadays, Big Tech corporations are training state of the art multi-billion parameter models on thousands of GPUs, spending millions of dollars on it, which the ordinary researcher cannot afford.

What I want to show with this project is that even for a non-profit research task, you can find like-minded volunteers and train a fairly large machine learning model.

The main goal of the project is to study the possibility of using LLM to “read” meaningful text in columns that can be compiled for a Running Key Cipher. The second goal is to train a fairly large model in a distributed manner with the help of volunteers from around the globe.



💡 Task Definition

Notations

For a clearer explanation of the problem, let me introduce the following concepts.

Let \(A\) be the alphabet of the English language, the letters of which are arranged in natural order. The \(\alpha + \gamma = \beta \,\) notation will be understood as the modular addition of letter numbers from \(\{ 0, \, 1, \, 2, \, ... \, , \, |A|- 1 \}\) modulo \(|A|\), where \(\alpha, \, \gamma, \, \beta \in A\). That is, when encrypting plaintext, we will identify letters with their numbers in the alphabet \(A\).

Simple case

Let's consider a simple example in which only two letters \(\gamma', \, \gamma'' \in A\) can be used as a keystream \(\bar{\gamma}=(\gamma_1, \, \gamma_2, \, … \, , \, \gamma_n)\) values, that is, the ciphertext \(\bar{\beta}=(\beta_1, \, \beta_2, \, … \, , \, \beta_n)\) formation equation has the form \(\alpha_i + \gamma_i = \beta_i, \; i \in \{1, \, 2, \, … \, , \, n\}\), where \(n\) is the length of the message. In this case, recovering the plaintext \(\bar{\alpha}=(\alpha_1, \, \alpha_2, \, ... \, , \, \alpha_n)\) by ciphertext \(\bar{\beta}\) isn't difficult. Indeed, we will make up the columns \(\bar{\nabla}=(\bar{\nabla_1}, \, \bar{\nabla_2}, \, ... \, , \, \bar{\nabla_n})\) according to the known ciphertext \(\bar{\beta}\), where \(\bar{\nabla_i}=(\beta_i-\gamma', \, \beta_i-\gamma''), \; i \in \{1, \, 2, \, ... \, , \, n\}\):

\(\beta_1-\gamma'\)\(\beta_2-\gamma'\)\(\beta_3-\gamma'\)\(...\)\(\beta_n-\gamma'\)
\(\beta_1-\gamma''\)\(\beta_2-\gamma''\)\(\beta_3-\gamma''\)\(...\)\(\beta_n-\gamma''\)

Obviously, each column \(\bar{\nabla_i} \) consists of unique values and contains one letter \(\alpha_i \) of the plaintext \(\bar{\alpha} \). You can try to recover this text using its redundancy. Without going into details, here is one example for “reading” in columns:

\(c\)\(d\)\(l\)\(p\)\(q\)\(o\)\(k\)\(u\)\(a\)\(x\)\(h\)\(g\)
\(y\)\(r\)\(y\)\(w\)\(t\)\(j\)\(g\)\(r\)\(b\)\(p\)\(m\)\(y\)
Have you read the word ...

cryptography 😉?

If four letters were used for encryption, then the column depth would be equal to four. And if all the letters were used, then the depth of the columns would be equal to \(|A|\) and in this case you can read any text in them.

General case

Let's take a closer look at an example in which all letters from the alphabet \(A\) can be used as keystream \(\bar{\gamma}\) values. In this case, there are also certain approaches for making up the columns \(\bar{\nabla}\). One of them is that in each column \(\bar{\nabla_i}=(\alpha_i^{(1)}, \, \alpha_i^{(2)}, \, ... \, , \, \alpha_i^{(|A|)})\) the order of possible plaintext letters \(\alpha_i^{(j)} \in A\) is determined by decreasing (more precisely, not increasing) their probabilities: \[P(\alpha_i^{(j)} \, | \, \beta_i) = \frac{P(\alpha_i^{(j)}, \, \beta_i)}{P(\beta_i)}=\frac{\phi(\alpha_i^{(j)}) \cdot \varphi(\beta_i-\alpha_i^{(j)})}{\sum_{\alpha’ \in A} \phi(\alpha’) \cdot \varphi(\beta_i-\alpha’)},\] \[i \in \{1, \, 2, \, ... \, , \, n\}, \; j \in \{1, \, 2, \, ... \, , \, |A|\},\] with a known fixed letter \(\beta_i \in A\) of the ciphertext \(\bar{\beta}\). Here \(\phi(\alpha), \; \alpha \in A\) is probability distribution of letters of meaningful texts for the alphabet \(A, \; \varphi (\gamma), \, \gamma \in A\) is probability distribution of the \(\bar{\gamma}\) keystream values.

Also, for a more accurate ordering of letters in columns, their probabilities are calculated based on n-grams.

Depth limitation

The depth \(\bar{h}=(h_1, \, h_2, \, ... \, , \, h_n)\) of the columns \(\bar{\nabla}=(\bar{\nabla_1}, \, \bar{\nabla_2}, \, ... \, , \, \bar{\nabla_n})\) can be limited using a pre-selected value of the \(\epsilon \in (0, 1]\) parameter: \[\begin{aligned} h_i=max\{\ell \in \{ 1, \, 2, \, ... \, , \, |A|\} : \sum_{j=1}^{\ell} P(\alpha_i^{(j)} \, | \, \beta_i) \le \epsilon \}. \end{aligned}\]

The critical depth of the columns \(\hat{h}\), at which it is possible to unambiguously determine the original plaintext, is calculated by the formula: \[\begin{aligned} \hat{h}=|A|^{1 - H(A)}, \end{aligned}\] where \(H(A)\) is entropy of a language with the \(A\) alphabet.

For English, \(\hat{h} \approx 13\).



👀 Demo

You can play with a pre-trained model hosted on HuggingFace Sphere.

Use the command below to run the service via Docker Compose.

docker-compose -f docker/compose/all-in-one-service.yml up

docker-compose -f docker/compose/scalable-service.yml up

trecover download artifacts
docker-compose -f docker/compose/all-in-one-service-duild.yml up --build

trecover download artifacts
docker-compose -f docker/compose/scalable-service-build.yml up --build


You can also try the Play with Docker service mentioned in the official docker documentation .

To run the service locally, docker must be installed. 

// Install the package
$ pip install trecover[demo]
<b>Successfully installed trecover</b>
<br>
// Initialize project's environment
$ trecover init
<b>Project's environment is initialized.</b>
<br>
// Download pretrained model
$ trecover download artifacts
<b>Downloaded "model.pt" to ../inference/model.pt</b>
<b>Downloaded "config.json" to ../inference/config.json</b>
<br>
// Start the service
$ trecover up
<b>🚀 The service is started</b>

❔ For more information use trecover --help or read the reference.

You can load the pre-trained model directly from the python script.

import torch

device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
model = torch.hub.load('alex-snd/TRecover', model='trecover', device=device, version='latest')

To print a help message and available pre-trained models run this:

import torch

print(torch.hub.help('alex-snd/TRecover', model='trecover', force_reload=True))
Do you want to challenge yourself ? 😉

Try to read meaningful text in these columns: 

a   d   f   o   n   p   p   u   w   f   o   u   d   d   y   k   d   d   a   u   n   t   r   y   x   g   n   k   w   n   t   n   t   t   a   t   t   u   r   e   t   g   t   x   r   u   e   w   r   t   h   n   x   o   d   v   t   i   t   i   o   t   p   f   m   o   b   k   j   z   t   g   d   s   c   y   w   w   w   t   d   x   h   k   n   d   p   d   a   r   d   x   d   n   g   t   h   p   u   r   w   u   n   d   d   n   z
    s   p   f   g       g   e   a   r           n   g   r   h   e   h   o       w   l       z   w   c   g   l   i   f       o   p   c   e   w   w   r   e           y       g   c   b       l       y       w   d       n       h   k   k           w   s   r   o   e       u   s   i   n   e   g       i   s   h   n   p   h   n   v   u   v   b   o   b   u           z   a   u   x   p   p       i   i       b   i       w   k   k   s
        z   e   k       h       q   l           x   r   t   o   u   y           z   e       p   a   e   e   q   q   p           g   f       a                       u       o       h       e               p   s       h       i   c   u           n       i               i   q       y       r       o       i   e       l   p   p   r   e   f   m   e   s           r   c       k   u   i       e   m       h           g   e   w   
        i       h       l           q           r       s       a   s           h           e   b       r   t       r           q   h       s                       t               q                       e   c       e       r   q   o                   o               q           e       q       e       c           o   r   y   l   a   p   e   a   m           q   e       u   l                       r           p   i   h   
        q       b                   j           m       c       s   c           y               c           o       s                                               s                                       a           l                                                   t                   s                               s   r   m   j           j   o           s           a   c                       j               o   q   
                o                   o                   o       m                                                   o                                               m                                       q           m                                                   b                                                   c   t                                   m           i   m                                           s

And see what the pre-trained model will recover:

1. Copy these columns 

a ds fpziq ofe ngkhbo p pghl ue waq frlqjo o u dnxrm dgr yrtsco kho deuasm dhysc ao u nwzhy tle r yzpe xwabc gce nger klqto wiq nfprso t no tpgq tcfh ae twas tw ur re e t gyutsm t xgo rc ubhq e wle r ty h nwpeaq xdsc o dnhelm v thir ikcq tkuo i o twn ps frio mo oe b kuiqtb jsq zi tnye ge dgrqs s cioe ys whic wne wp thlo dnprsc xvpyrt hurlm kveaj nbfp dome pbeaj dusmo a r dzrqsm xace du nxkuai gpulcm tpi h pie uim r wbhrj ui n dwgp dkeio nkwhqs zs

2. Open the dashboard hosted here

3. In the sidebar, select "Noisy columns" as an input type

4. Paste the copied columns into the input field

5. Click the "Recover" button 🎉



💪 Join Collaborative Training

😎 Easy way

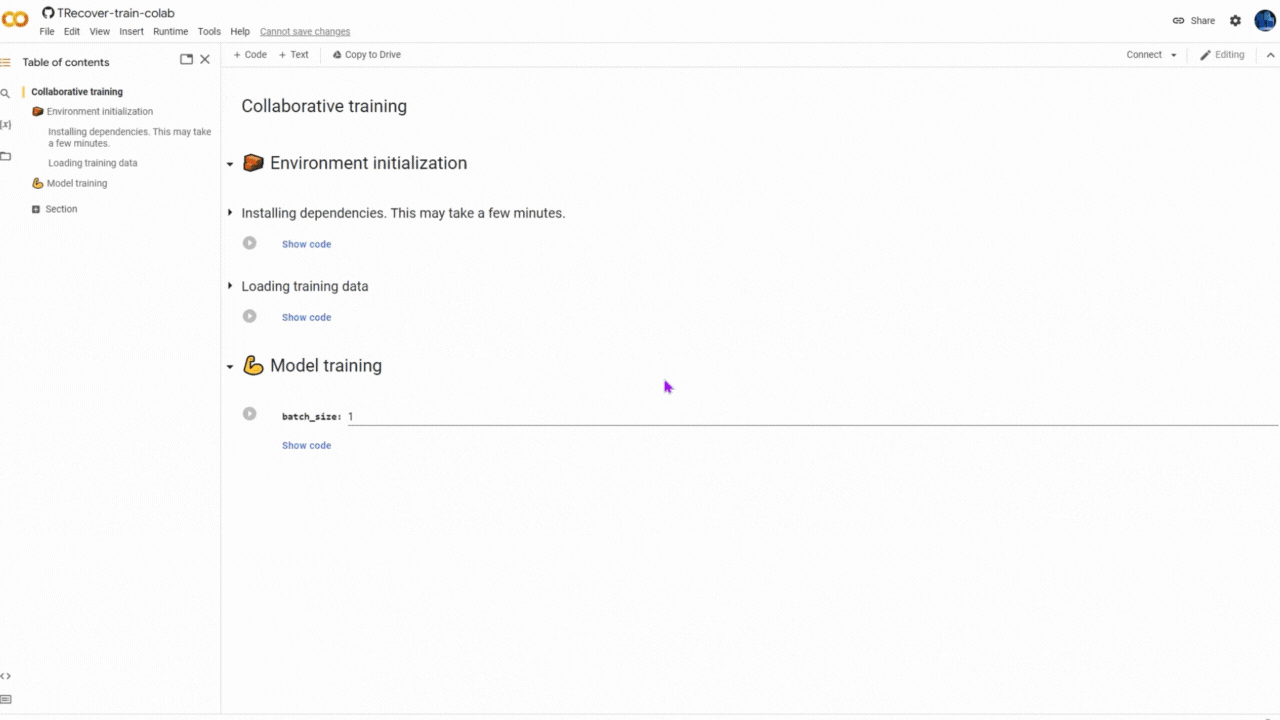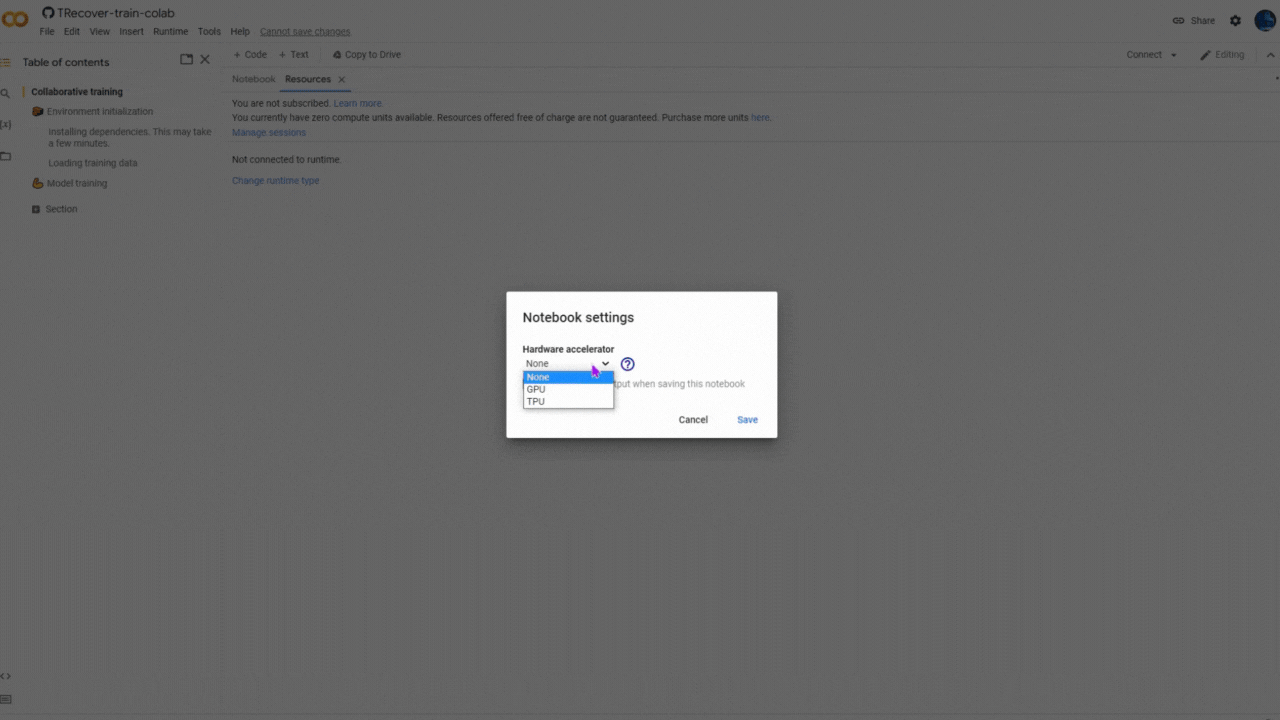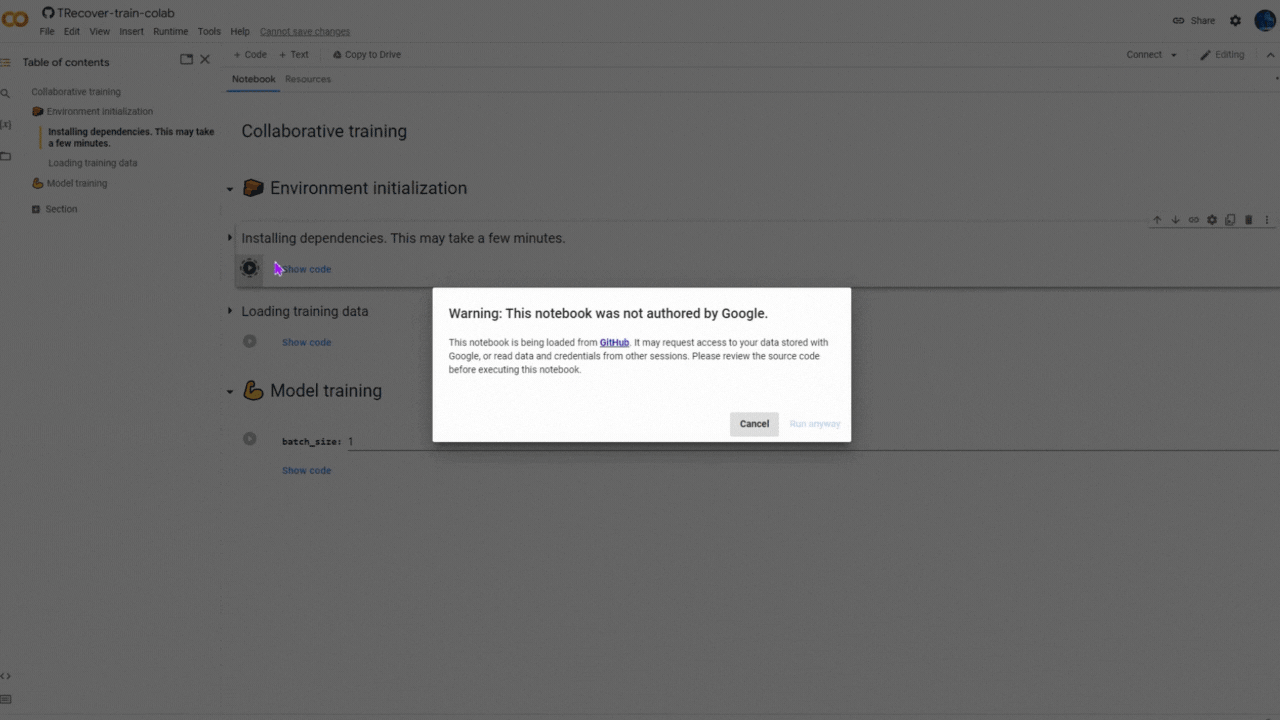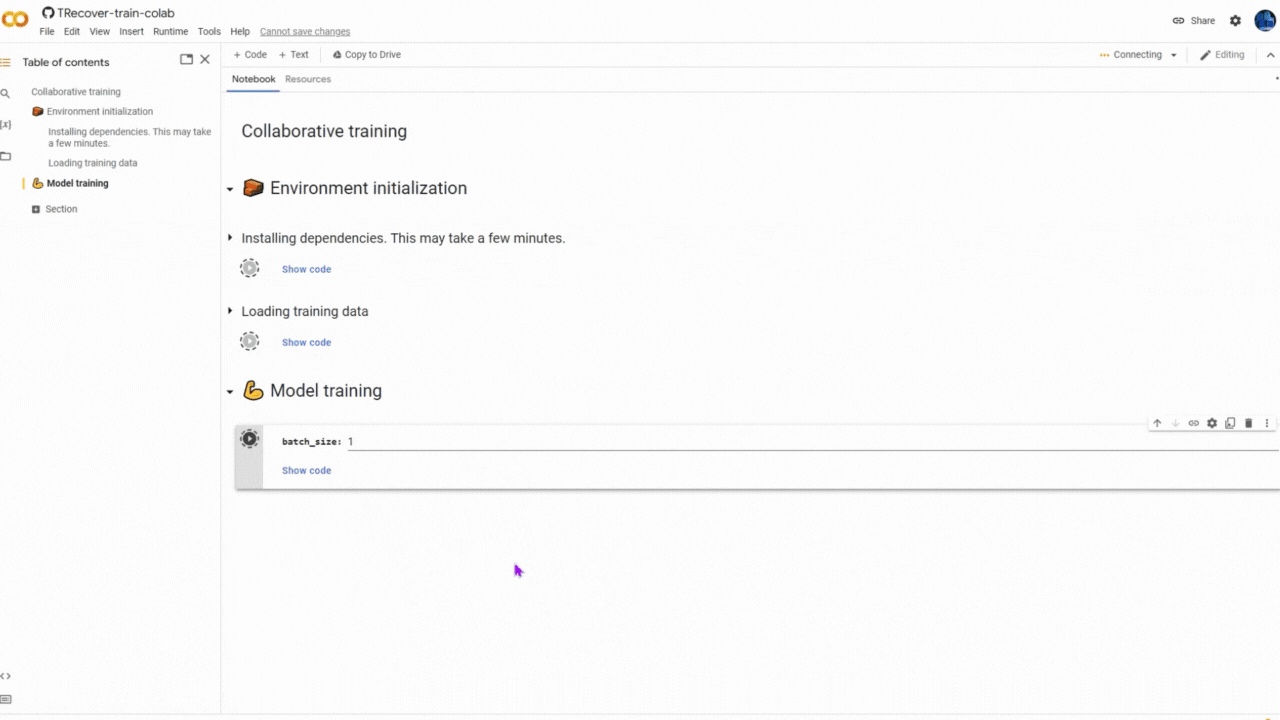
You can help to train the model by running a pre-prepared Jupyter Notebook on Kaggle or Google Colab. To join the collaborative training, all you have to do is to keep the Notebook running for at least 15 minutes (but more is better) and you're free to close it after that and join again in another time.

Join as a client peer

Kaggle gives you around 40 hrs per week of GPU time, so it's preferred over Colab, unless you have Colab Pro or Colab Pro+.

Please make sure to select GPU accelerator and switch the "Internet" ON, in kernel settings

If you are a new Kaggle member, you will need to verify your phone number in the settings pane to turn on the Internet.

Warning: please don't use multiple Kaggle accounts at once

Please make sure to select GPU accelerator

Warning: please don't use multiple Google Colab accounts at once

😊 Preferred way

You can join the collaborative training as an auxiliary peer if you have a Linux computer with 15+ GB RAM, at least 100 Mbit/s download&upload speed and one port opened to incoming connections. Also, if in addition to all this there is also a GPU, then you can join as a trainer peer.

Why is this way more preferable?

There are two broad types of peers: normal (full) peers and client mode peers. Client peers rely on others to average their gradients, but otherwise behave the same as full peers. This way of participation is preferable as the auxiliary and trainer peers not only don’t rely on others, but also can serve as relays and help others with all-reduce.

Installation

This step is common to the trainer and auxiliary peer, and requires Python 3.8 or higher. Open a tmux (or screen) session that will stay up after you logout and follow the instructions below. 

// Clone the repository
$ git clone https://github.com/alex-snd/TRecover.git
Cloning into 'TRecover'...    
remote: Enumerating objects: 4716, done.
remote: Counting objects: 100% (368/368), done.
remote: Compressing objects: 100% (133/133), done.
remote: Total 4716 (delta 196), reused 348 (delta 181)
---> 100%
Receiving objects: 100% (4716/4716), 18.69 MiB | 4.36 MiB/s, done.
Resolving deltas: 100% (2908/2908), done.
<br>
// Change the working dir
$ cd TRecover
<br>
// Create a virtual environment
$ python3 -m venv venv
<br>
// Activate the virtual environment
$ source venv/bin/activate
<br>
// Install the package
$ pip install -e .[collab]
<b>Successfully installed trecover</b>
<br>
// Initialize project's environment
$ trecover init
<b>Project's environment is initialized.</b>
<br>
<br>
// For more information use <font color="#36464E">trecover --help</font> or read the <a href="https://alex-snd.github.io/TRecover/src/trecover/app/cli">reference</a>.

Join as a trainer peer

Trainers are peers with GPUs (or other compute accelerators) that compute gradients, average them via all-reduce and perform optimizer steps. 

// Download the train dataset
$ trecover download data
---> 100%
Downloaded "data.zip" to ../data/data.zip
Archive extracted to ../data

// Run the trainer peer
$ trecover collab train --sync-args --batch-size 1 --n-workers 2 --backup-every-step 1

// Use <font color="#36464E">--help</font> flag for more details

Join as an auxiliary peer

Auxiliary peers are low-end servers without GPU that will keep track of the latest model checkpoint and assist in gradient averaging. 

// Run the auxiliary peer
$ trecover collab aux --sync-args --verbose --as-active-peer --backup-every-step 1

// Use <font color="#36464E">--help</font> flag for more details